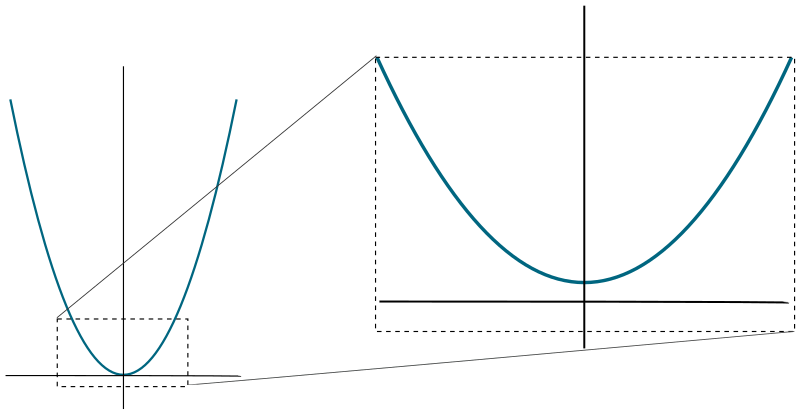
Todas las parábolas son semejantes, es únicamente la escala la que crea la apariencia de que tienen formas diferentes
Aunque la definición original de la parábola es la relativa a la sección de un cono recto por un plano paralelo a su directriz, actualmente es más común definir la parábola como un lugar geométrico:
|
De esta forma, una vez fija una recta y un punto se puede construir una parábola que los tenga por foco y directriz de acuerdo a la siguiente construcción. Sea T un punto cualquiera de la recta directriz. Se une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se puede aproximar tantos puntos de la parábola como sea necesario.
De la construcción anterior se puede probar que la parábola es simétrica respecto a la línea perpendicular a la directriz y que pasa por el foco. Al punto de intersección de la parábola con tal línea (conocida como eje de la parábola) se le conoce como vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como Distancia focal o Radio focal.
Lado recto
Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.
|
Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).
Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.
[editar]Semejanza de todas las parábolas
Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad e = 1. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.
[editar]Tangentes a la parábola
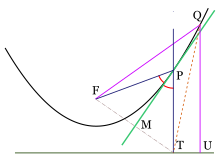
Un resultado importante en relación a las tangentes de una parábola establece:
|
En lo sucesivo, F denotará el foco de una parábola, P un punto de la misma y T su proyección sobre la directriz. Retomando la construcción dada para encontrar puntos de una parábola, sea MP la mediatriz del triángulo FPT, el cual es isósceles y por tanto biseca al ángulo FPT. Lo único que hay que verificar ahora es que MP también es la tangente en el punto P. Sea Q otro punto de la parábola y sea U su proyección en la directriz.
Puesto que FQ=QU y QU<QT, entonces FQ<QT. Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta MP, esto quiere decir que MP es la tangente de la parábola en P.