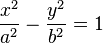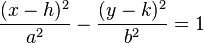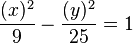ECUACIONES DE LA HIPERBOLA
Ecuaciones en coordenadas cartecianas: Ecuación de una hipérbola con centro en el origen de coordenadas 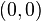 y ecuación de la hipérbola en su forma compleja.
y ecuación de la hipérbola en su forma compleja.
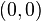 y ecuación de la hipérbola en su forma compleja.
y ecuación de la hipérbola en su forma compleja.Ecuación de una hipérbola con centro en el punto 

Ejemplos:
a)
b)
Ecuación de la hipérbola en su forma compleja
Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos  , en el plano
, en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias
; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 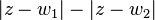 , a dos puntos fijos llamados focos
, a dos puntos fijos llamados focos y
y  , es una costante positiva igual al doble de la distancia (osea
, es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
) que existe entre su centro y cualesquiera de sus vértices del eje focal.
 , en el plano
, en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias
; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 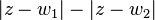 , a dos puntos fijos llamados focos
, a dos puntos fijos llamados focos y
y  , es una costante positiva igual al doble de la distancia (osea
, es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
) que existe entre su centro y cualesquiera de sus vértices del eje focal.La ecuacion queda: 

Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.